Interpolační polynomy
Jednou ze základních úloh numerických metod matematické analýzy jsou aproximace reálných funkcí. Aproximovat funkci znamená nalézt vhodnou lineární kombinaci předem zadaných funkcí, která bude v jistém smyslu blízká zadané funkci. Bude se snadno matematicky zpracovávat a bude vhodná pro počítačové zpracování. Pro řadu funkcí jsou tyto aproximace již zpracovány, jsou součástí matematických software a běžně je používáme na počítačích i kapesních kalkulačkách.
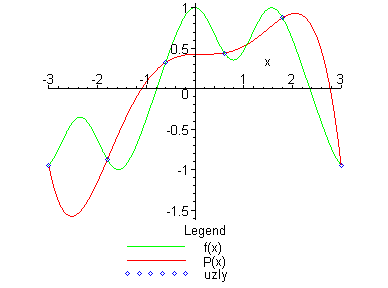
Speciálním případem aproximace je interpolace interpolačním polynomem. Interpolační polynom má tu vlastnost, že se s funkcí f shoduje v předem daných bodech = uzlech..
Předpokládejme, že funkce f je dána tabulkou hodnot v uzlových bodech.
| xi | x1 | x2 | x3 | ... | xk |
| fi | f1 | f2 | f3 | ... | fk |
Naším úkolem bude nalézt polynom P tak, aby platilo:
P(xi) = fi

Polynom P bude mít obecně tvar
P(x) = c1 + c2x + c3x2 + ... + ck xk-1
kde c1 ... ck budou neznámé konstanty.
Z podmínek P(xi) = fi , i = 1, ..., k postupně dostaneme
| c1 + c2x1 + c3x12 + ... + ck x1k-1 | = f1, |
| c1 + c2x2 + c3x22 + ... + ck x2k-1 | = f2, |
| ... | |
| c1 + c2xk + c3xk2 + ... + ck xkk-1 | = fk, |
což je soustava k rovnic o k neznámých. Tato soustava má právě jedno řešení c1 ... ck.
Abychom se vyhnuli řešení této soustavy, postupujeme při hledání interpolačního polynomu většinou jiným způsobem. Podle způsobů konstrukce tohoto polynomu nazýváme pak tento polynom ...
Lagrangerův interpolační polynom
... nebo ...
Newtonův interpolační polynom
... apod.
Jedná se však vždy o stejný polynom.
Příklady
Animace