Postup konstrukce s využitím Maplu
Jsou dána čísla x1 ... xk a f1 ... fk .
>
k:=5:
body:=array(1..k,[[x[1],f[1]],[x[2],f[2]],[x[3],f[3]],[x[4],f[4]],[x[5],f[5]]]);
![]()
Hledáme polynom L(x) takový, pro který platí
L(xi) = fi
Lagrangerův polynom L(x) bude ve tvaru
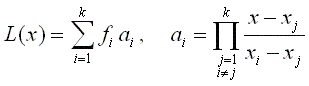
kde ai nazýváme bázové funkce.
>
a:=array(1..k):
for i from 1 by 1 to k do
a[i]:= product( (x-body[j][1])/(body[i][1]-body[j][1]), j=1..i-1 )*
product( (x-body[j][1])/(body[i][1]-body[j][1]), j=i+1..k )
od;
![a[1] := (x-x[2])/(x[1]-x[2])*(x-x[3])/(x[1]-x[3])*(...](Images/Lagrange_postup/interpolacni_krivky_proc11.gif)
![a[2] := (x-x[1])/(x[2]-x[1])*(x-x[3])/(x[2]-x[3])*(...](Images/Lagrange_postup/interpolacni_krivky_proc12.gif)
![a[3] := (x-x[1])/(x[3]-x[1])*(x-x[2])/(x[3]-x[2])*(...](Images/Lagrange_postup/interpolacni_krivky_proc13.gif)
![a[4] := (x-x[1])/(x[4]-x[1])*(x-x[2])/(x[4]-x[2])*(...](Images/Lagrange_postup/interpolacni_krivky_proc14.gif)
![a[5] := (x-x[1])/(x[5]-x[1])*(x-x[2])/(x[5]-x[2])*(...](Images/Lagrange_postup/interpolacni_krivky_proc15.gif)
Pro dané k bude mít výsledný polynom tvar
> L(x):=sum(body[n][2]*a[n], n=1..k);
![L(x) := f[1]*(x-x[2])/(x[1]-x[2])*(x-x[3])/(x[1]-x[...](Images/Lagrange_postup/interpolacni_krivky_proc16.gif)
![L(x) := f[1]*(x-x[2])/(x[1]-x[2])*(x-x[3])/(x[1]-x[...](Images/Lagrange_postup/interpolacni_krivky_proc17.gif)
procedura Lagrange()