Příklady

1. příklad:

> k:=4:
    body:=array(1..k,[[0,0],[1,3],[2,1],[3,3]]);

... a naším úkolem je najít takový polynom, který by procházel všemi uzlovými body.

> a:=array(1..k):
    for i from 1 by 1 to k do
        a[i]:= product( (x-body[j][1])/(body[i][1]-body[j][1]), j=1..i-1 )*
                  product( (x-body[j][1])/(body[i][1]-body[j][1]), j=i+1..k )
    od;

> L(x):=sum(body[n][2]*a[n], n=1..k);

> L(x):=expand(L(x));

> plots[display]({plot(body,x=body[1][1]..body[k][1],style=point,color=blue),
                            plot(L(x),x=body[1][1]..body[k][1],style=line,color=red)
                          });

2. příklad:

Vytvořme si tabulku funkce f(x)  = sin(x) na intervalu <-Pi ; Pi> tak, že ji tabelujeme s krokem Pi/2.

> k:=5:
    body:=[seq([a+i*(b-a)/(k-1),f(a+i*(b-a)/(k-1))],i=0..k-1)];

A nyní budeme funkci danou touto tabulkou interpolovat Lagrangerovým interpolačním polynomem čtvrtého stupně. Vytvoříme bázové funkce  a₁ ... a₅ ...

> a:=array(1..k):
    for i from 1 by 1 to k do
        a[i]:= product( (x-body[j][1])/(body[i][1]-body[j][1]), j=1..i-1 )*
                  product( (x-body[j][1])/(body[i][1]-body[j][1]), j=i+1..k )
    od;

... a dosazením do vzorce získáme ...

> L(x):=sum(body[n][2]*a[n], n=1..k);

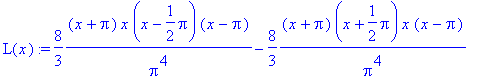
... po zjednodušení ...

> L(x):=expand(L(x));

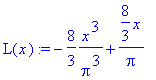
Na grafech je vidět, že přestože náš polynom přesně neodpovídá funkci sin(x), jeho graf opět prochází zvolenými uzlovými body.

> plots[display]({plot(body,x=body[1][1]..body[k][1],style=point,color=blue),
                            plot(L(x),x=body[1][1]..body[k][1],style=line,color=red),
                            plot(f(x),x=body[1][1]..body[k][1],style=line,color=green)
                          });