interpolacni.html

Postup konstrukce s využitím Maplu

Jsou dána čísla x₁ ... x_k a f₁ ... f_k .

> k:=5:
body:=array(1..k,[[x[1],f[1]],[x[2],f[2]],[x[3],f[3]],[x[4],f[4]],[x[5],f[5]]]);

Hledáme polynom N(x) takový, pro který platí

N(x_i) = f_i

Newtonů polynom N(x) bude ve tvaru

N(x) =
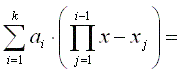=	a₁ + a₂(x - x₁) + a₃(x - x₁)(x - x₂) + ... + a_k(x - x*₁)(x - x₂) ...* (x - x_k-₁)**

Víme, že musí platit N(x_i) = f_i . Koeficienty a_i spočítáme ze soustavy rovnic, kterou získáme postupným dosazováním x_i do předcházející rovnosti.

...

+ ... +

Matice této soustavy bude vypadat takto

> A:=array(1..k,1..k):
    for i from 1 by 1 to k do
        A[i,1]:=1:
    end do:
    for i from 1 by 1 to k do
        for j from 2 by 1 to k do
            A[i,j]:=0:
        end do:
    end do:
    f(y):=1:
    for j from 2 by 1 to k do
        f(y):=f(y)*(y-body[j-1][1]):
        for i from j by 1 to k do
            A[i,j]:=eval(f(y),y=body[i][1]):
        end do:
    end do:
eval(A);

... se sloupcem pravých stran ...

> B:=array(1..k):
    for i from 1 by 1 to k do
        B[i]:=body[i][2]:
    end do:
    eval(B);

procedura Newton()