Příklady
1. příklad:
Funkce f je dána tabulkou ...
| xi | 0 | 1 | 2 | 3 |
| fi | 0 | 3 | 1 | 3 |
>
k:=4:
body:=array(1..k,[[0,0],[1,3],[2,1],[3,3]]);
![]()
... a naším úkolem je opět najít takový polynom, který by procházel všemi uzlovými body.
Podle předcházejícího postupu zkonstruujeme Newtonův interpolační polynom.
Ze zadaných bodů sestrojíme příslušnou soustavu 4 rovnic o 4 neznámých ...
>
A:=array(1..k,1..k):
for i from 1 by 1 to k do
A[i,1]:=1:
end do:
for i from 1 by 1 to k do
for j from 2 by 1 to k do
A[i,j]:=0:
end do:
end do:
f(y):=1:
for j from 2 by 1 to k do
f(y):=f(y)*(y-body[j-1][1]):
for i from j by 1 to k do
A[i,j]:=eval(f(y),y=body[i][1]):
end do:
end do:
eval(A);
![matrix([[1, 0, 0, 0], [1, 1, 0, 0], [1, 2, 2, 0], [...](Images/Newton_priklady/interpolacni2.gif)
>
B:=array(1..k):
for i from 1 by 1 to k do
B[i]:=body[i][2]:
end do:
eval(B);
![]()
... a vyřešíme ji.
> a:=linsolve(A,B);
![]()
Nelezené řešení, tedy koeficienty a1 ... a4 už můžeme dosadit do vzorce ...
> N(x):=sum(a[n]*product((x-body[m][1]),m=1..n-1), n=1..k);
![]()
... a zjednodušit.
> N(x):=expand(N(x));
![]()
Graf opravdu prochází všemi čtyřmi zadanými uzlovými body.
>
plots[display]({plot(body,x=body[1][1]..body[k][1],style=point,color=blue),
plot(N(x),x=body[1][1]..body[k][1],style=line,color=red)
});
![[Maple Plot]](Images/Newton_priklady/interpolacni7.gif)
2. příklad:
Vytvořme si tabulku funkce f(x) = sin(x) na intervalu <-Pi ; Pi> tak, že ji tabelujeme s krokem Pi/2.
>
k:=5:
body:=[seq([a+i*(b-a)/(k-1),f(a+i*(b-a)/(k-1))],i=0..k-1)];
![]()
Z vybraných uzlových bodů vyrobíme příslušnou soustavu 5 rovnic o 5 neznámých ...
>
A:=array(1..k,1..k):
for i from 1 by 1 to k do
A[i,1]:=1:
end do:
for i from 1 by 1 to k do
for j from 2 by 1 to k do
A[i,j]:=0:
end do:
end do:
f(y):=1:
for j from 2 by 1 to k do
f(y):=f(y)*(y-body[j-1][1]):
for i from j by 1 to k do
A[i,j]:=eval(f(y),y=body[i][1]):
end do:
end do:
eval(A);
![matrix([[1, 0, 0, 0, 0], [1, 1/2*Pi, 0, 0, 0], [1, ...](Images/Newton_priklady/interpolacni9.gif)
>
B:=array(1..k):
for i from 1 by 1 to k do
B[i]:=body[i][2]:
end do:
eval(B);
![]()
... a vyřešíme.
> a:=linsolve(A,B);
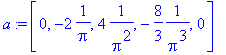
Řešení opět dosadíme do vzorce ...
> N(x):=sum(a[n]*product((x-body[m][1]),m=1..n-1), n=1..k);
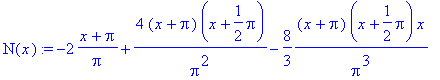
... a nakonec ještě zjdnodušíme.
> N(x):=expand(N(x));
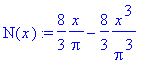
Graf nalezeného polynomu opravdu v uzlových bodech protíná graf funkce sin(x).
>
plots[display]({plot(body,x=body[1][1]..body[k][1],style=point,color=blue),
plot(N(x),x=body[1][1]..body[k][1],style=line,color=red),
plot(f(x),x=body[1][1]..body[k][1],style=line,color=green)
});
![[Maple Plot]](Images/Newton_priklady/interpolacni14.gif)
Soubor v Maplu: newton_priklady.mws