Aplety v programu GeoGebra

Planimetrie - Množiny všech bodů dané vlastnosti - Brankářská množina

Množina bodů, z nichž je vidět úsečka AB pod daným úhlem γ

Všimněte si, že vrcholy úhlu zvoleného tak, aby měl danou velikost γ a aby jeho ramena procházela body A, B, vytvářejí dvojici kruhových oblouků, jejichž středy leží na ose úsečky AB. Takovéto úhly se nazývají obvodové, neboť jejich vrcholy leží na obvodu oblouku. Pro jejich velikost platí, že je rovna polovině příslušného středového úhlu ASB.

(Můžeš se vrátit k apletu na středové a obvodové úhly)

Množinu vrcholů úhlů, z nichž je úsečka AB vidět pod úhlem o velikosti γ lze zapsat takto:

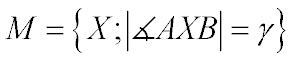
Zapamatujte si i čtení takovéhoto zápisu:
„M je množinou bodů (roviny), pro které platí, že velikost úhlu AXB je γ.“

Poznámka: Je vidět, že pro úhel γ = 90° je BRANKÁŘSKOU MNOŽINOU vlastně THALETOVA KRUŽNICE. (Thales byl vynikající brankář antického fotbalu.)

1) Nejprve sestrojte osu úsečky AB.

2) Od úsečky AB do jedné poloroviny vyneste tzv. úsekový úhel s vrcholem v bodě A, jehož velikost je rovna velikosti γ. Vznikne polopřímka AM.

3) K ní veďte kolmici bodem A. Ta vymezí na ose
úsečky střed hledaného oblouku k1 – bod S, poloměr oblouku je SA, resp.SB.

4) Sestrojíme oblouk k1.

5) Máme tedy sestrojenou jednu část hledané množiny – oblouk k1. Druhý
oblouk k2 včetně jeho středu sestrojíte osově souměrně podle přímky AB.

Hledanou množinu tvoří sjednocení dvou oblouků k1 a k2, přičemž do ní nepatří body A a B.

Poznámka: Konstrukci si prakticky vyzkoušejte – například pro úhly 30°, 45°, 60°. Měli byste ji ovládat zpaměti, obdobně jako například některý důležitý algebraický vzorec!!!

Konstrukce množiny bodů, z nichž vidíme úsečku AB pod tupým úhlem γ:

Postup je v podstatě stejný jako u ostrého úhlu.
1) Od AB nanesete úsekový úhel velikosti γ.

2) K jeho ramenu AM sestrojíte kolmici bodem A, ta protne osu úsečky v bodě S.

3) Oblouk, který je v tomto případě menší než půlkružnice, má střed S a poloměr SA, resp. SB.

4) Druhý oblouk bude s ním osově souměrný podle
AB.

Zdůvodnění správnosti konstrukce: