Inerciální a neinerciální vztažné soustavy

Na úvod trochu teorie

V přírodě rozeznáváme čtyři druhy vzájemného silového působení - interakcí. Jsou to interakce:

• elektromagnetická
• gravitační
• silná jaderná
• slabá jaderná

Jaderné interakce se projevují pouze v rozměrech srovnatelných s rozměrem jádra atomu  10^–15m  a zde se jimi nebudeme dále zabývat. Gravitační interakce způsobuje všeobecné přitahování hmotných těles gravitační silou  F_g = κ.m₁.m₂/r² , kde κ=6,67.10^–11N.m²kg^–2 je gravitační konstanta, m₁ a m₂ hmotnosti těles a r vzdálenost jejich středů. Na povrchu Země jsou tělesa přitahována silou tíhovou  F_G = m.g , kde m je hmotnost tělesa a g je tíhové zrychlení (přibližně 9,8 m.s^–2). Tíhová síla je výslednicí síly gravitační a síly odstředivé dané tím, že Země se otáčí a soustava spojená se Zemí je neinerciální. Z kvantitativního hlediska není síla odstředivá v tomto případě příliš významná. Elektromagnetická interakce způsobuje jednak elektromagnetické jevy na makroskopické úrovni, ale též způsobuje vazby mezi částicemi látky (molekulami navzájem, atomy v molekulách, elektrony a atomovými jádry). Síly pevnosti materiálu a síly třecí a odporové jsou proto elektromagnetické povahy. Působením výše popsaných sil můžeme s použitím Newtonových pohybových zákonů vysvětlit jakýkoli mechanický pohyb, který se odehrává v inerciální soustavě. Jedním ze základních principů fyziky je tvrzení, že takováto soustava existuje.

Inerciální soustava je soustava, ve které můžeme vysvětlit libovolný makroskopický pohyb podle Newtonových zákonů na základě působení gravitačních a elektromagnetických sil.

Každá soustava, která se vzhledem k nějaké inerciální soustavě pohybuje rovnoměrně přímočaře, je také inerciální.

Soustavy, které se vzhledem k inerciální soustavě pohybují se zrychlením nebo se otáčejí, jsou neinerciální.

Neinerciální soustava je soustava, která není inerciální.

Pokud v takových soustavách chceme vysvětlit pohyby těles a současně udržet platnost druhého Newtonova zákona, musíme zavést další síly (setrvačnou, odstředivou a Coriolisovu). O společný název těchto sil se vedou v literatuře spory. Říkejme jim třeba síly neinerciální. Projevují se v těchto případech:

Setrvačná síla - působí na všechny hmotné body (HB) v soustavách, které se pohybují se zrychlením. Platí pro ni vztah  F_S = −m.a_S , kde m je hmotnost HB, na nějž síla působí, a a_S je zrychlení soustavy. Vztah je vektorový a udává, že setrvačná síla má opačný směr, než zrychlení soustavy.

Odstředivá síla - působí na všechny hmotné body v soustavách, které se otáčejí. Platí pro ni vztah  F_O = m.ω².r , kde m je hmotnost HB, na nějž síla působí, ω je úhlová rychlost otáčení neinerciální soustavy a r vektor kolmý na osu otáčení s počátečním bodem na této ose a koncovým bodem v daném HB. Odstředivá síla tedy míří od osy otáčení.

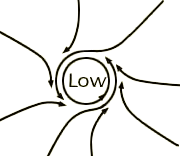
Coriolisova síla - působí na všechny hmotné body, které se pohybují v soustavách, jež se otáčejí. Platí pro ni vztah  F_C = 2m.(vxω) , kde m je hmotnost HB, ω je úhlová rychlost otáčení soustavy a v je vektor rychlosti HB v této soustavě. Pro velikost Coriolisovy síly plyne  F_C = 2m.v.ω.sin.α , kde α je úhel mezi vektory v a ω. Síla je kolmá k oběma vektorům a její směr určíme podle pravidla pravé ruky. Této síle se sice můžeme při výkladu v prvním ročníku vyhnout, ale také můžeme pomocí ní vysvětlit chování Foucaultova kyvadla nebo rozdílné stáčení tlakových výší a níží na severní a jižní polokouli, které studenti budou probírat v zeměpisu.

Obsah

Na úvod trochu teorie
Příklady
Nápověda k řešení úloh

Úlohy:
Brzdící vagón
úlohy:  I.   II.   III.   IV. 
Rozjíždějící se vagón
úlohy:  V.   VI.   VII.   VIII. 
Zatáčející vagón
úlohy:  IX.   X.   XI.   XII. 
Družice na oběžné dráze
úlohy:  XIII.   XIV. 
Beztížný stav v kosmické lodi
úlohy:  XV.   XVI. 
Střelba na otáčejícím se disku
úlohy:  XVII.   XVIII. 
Kolotoč a jeho okolí
úlohy:  XIX.   XX.