Inerciální a neinerciální vztažné soustavy

Příklady

1. Vysvětlete z dynamického hlediska pohyb družice o hmotnosti m rychlostí v kolem planety o hmotnosti M po kruhové trajektorii s poloměrem r.

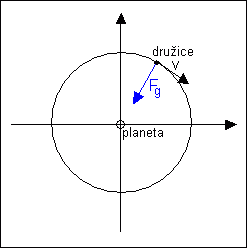a) Řešení v soustavě inerciální. Zvolme soustavu s počátkem ve středu planety, první osa míří ke Slunci, druhá je na ni kolmá. Tuto soustavu lze považovat za inerciální. Družice se v ní pohybuje po kružnici. Na družici působí gravitační síla planety F_g = κ.m.M / r². Tato síla způsobuje stáčení trajektorie do tvaru kružnice a je tedy silou dostředivou. Pohyb můžeme popsat rovnicí

F_g = F_d
κ.m.M / r² = m.v² / r

Žádná další síla na družici nepůsobí. Rozhodně na ni nepůsobí síla odstředivá, protože jsme v inerciální soustavě.

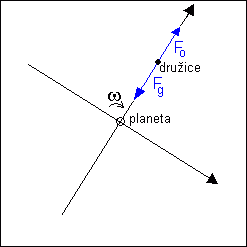b) Řešení v soustavě neinerciální. Zvolme soustavu s počátkem ve středu planety, první osa prochází družicí, druhá je na ni kolmá. Protože první osa stále prochází družicí, bude se tato soustava vzhledem k inerciální soustavě z minulého řešení otáčet s úhlovou rychlostí ω = v/r. Je to tedy soustava neinerciální. Družice se v  této soustavě nepohybuje. (osa prochází družicí a  družice je stále stejně vzdálena od počátku). Působí na ni gravitační síla planety (jde o sílu nezávislou na soustavě) a síla odstředivá F_o = m.ω².r = m.v²/r, která má původ v neinerciálnosti soustavy. Protože družice je v této soustavě v klidu, musí být tyto síly vyrovnány a platí rovnice

F_g = F_o
κ.m.M / r² = m.v² / r

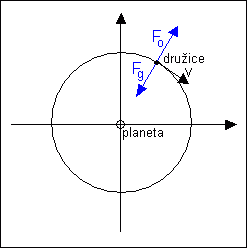c) Řešení nesprávné. Na družici působí gravitační síla F_g, a protože se družice pohybuje po kružnici, i odstředivá síla F_o. Tyto síly působí proti sobě a vzájemně se ruší, proto se družice pohybuje po ekvipotenciální ploše - zde po kružnici. Platí rovnice

F_g = F_o
κ.m.M / r² = m.v² / r

Přestože při tomto řešení dostaneme matematicky správnou rovnici a tedy jsme schopni vypočítat správné číselné hodnoty veličin, jde o řešení nesprávné z více důvodů. Pokud říkáme, že se družice pohybuje po kružnici, máme zřejmě na mysli soustavu inerciální a pak nemůžeme mluvit o odstředivé síle. Pokud bychom už existenci této síly připustili, a ona by se skutečně vyrušila se silou gravitační, pak by se družice ve shodě s prvním Newtonovým zákonem musela pohybovat po přímce a nic by ji nenutilo zatočit po kružnici.

2. Ve vagónu, který se rozjíždí pohybem rovnoměrně zrychleným se zrychlením a, je zavěšena kulička, která se vychýlí ze svislého směru o úhel φ . Popište působící síly.

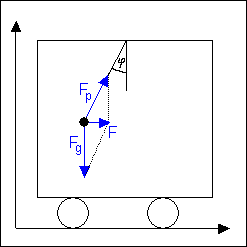a) Řešení v soustavě spojené s kolejemi - inerciální.

Na kuličku působí síla tíhová F_G = m.g a tah provázku  F_p (pevnost provázku má elektromagnetickou podstatu). Tyto síly vytvářejí výslednici  ve vodorovném směru F = m.a, protože kulička se spolu s vagónem pohybuje rovnoměrně zrychleně se zrychlením a. Platí:

tan φ = F / F_G = m.a / m.g = a / g

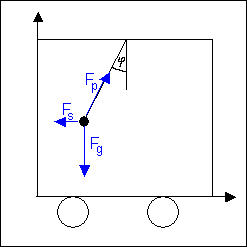b) Řešení v soustavě spojené s vagónem - neinerciální, protože vagón se pohybuje se zrychlením.

Na kuličku působí síla tíhová F_G = m.g, tah provázku F_p a síla setrvačná F_S = −m.a_S. Tyto tři síly jsou vzájemně vyrovnány, protože kulička je vzhledem k vagónu v klidu. Platí:

tan φ = F_S / F_G = m.a / m.g = a / g

Obsah

Na úvod trochu teorie
Příklady
Nápověda k řešení úloh

Úlohy:
Brzdící vagón
úlohy:  I.   II.   III.   IV. 
Rozjíždějící se vagón
úlohy:  V.   VI.   VII.   VIII. 
Zatáčející vagón
úlohy:  IX.   X.   XI.   XII. 
Družice na oběžné dráze
úlohy:  XIII.   XIV. 
Beztížný stav v kosmické lodi
úlohy:  XV.   XVI. 
Střelba na otáčejícím se disku
úlohy:  XVII.   XVIII. 
Kolotoč a jeho okolí
úlohy:  XIX.   XX.